記号の世界ゟ

このブログでは, 数学書などの書評を書きます。また、受験などの勉強法をまとめます。

一般化戸田方程式について

可積分

可積分な方程式のとして重要な戸田格子には様々な一般化があります．戸田格子の背後にある半単純リー代数の構造に着目し，戸田格子に類似する可積分な微分方程式を得る方法を紹介します．この視点に立てば，通常の戸田格子はA_n型の半単純リー代数に対応するものであると捉え直すことができます．

この記事ではハミルトン系とリー代数の定義は既知とします．（性質は記事の中で復習する．）

戸田格子

線形バネの格子


戸田格子のモチベーションを説明するために，まずは簡単な線形バネの場合から説明を始めます．


バネでつながれた n 個の質点を考えます．

f:id:tetobourbaki:20190812172123j:plain
バネでつながれた円周上の質点
質点は円状に配置されていて，隣り合う質点同士がバネでつながれているとします．バネ定数を k とするとハミルトニアンは
\displaystyle \qquad H = \frac{1}{2} \sum_{j=1}^n p_j^2 + \sum_{j=1}^{n-1} \frac{k}{2} (q_j - q_{j+1})^2 + \frac{k}{2} (q_n - q_1)^2
となります．記述を簡単にするために， q_{n+1} := q_1, q_0 := q_n と書くことにします．するとハミルトニアンは
\displaystyle \qquad H = \frac{1}{2} \sum_{j=1}^n p_j^2 + \sum_{j=1}^{n} \frac{k}{2} (q_j - q_{j+1})^2
と書き直すことができます．このとき，ハミルトン系は
\displaystyle\qquad \frac{d q_j}{d t} = p_j \\ \displaystyle \qquad \frac{d p_j}{d t} = -k (q_j - q_{j+1}) + k(q_{j-1} - q_j) = k ( q_{j-1} - 2 q_{j} + q_{j+1})
と書くことができます．線形の連立方程式なので，この方程式は解くことができます．

戸田格子


バネの力が線形にかかる場合を考えましたが，非線形の場合で解けることはあるのでしょうか？戸田盛和先生は解が楕円関数を使って書き下すことができる非線形の方程式を導きました．
\displaystyle \qquad H = \frac{1}{2} \sum_{j=1}^n p_j^2 + \sum_{j=1}^{n-1} \exp (q_j - q_{j+1}) + \exp (q_n - q_1) \\ \displaystyle \qquad \quad = \frac{1}{2} \sum_{j=1}^n p_j^2 + \sum_{j=1}^{n} \exp (q_j - q_{j+1})
このハミルトニアンが定める微分方程式を戸田格子と呼ぶことにします．最後の \exp (q_n - q_1) の項がない場合も戸田格子と呼ばれます．


微分方程式の可積分性は微分方程式論の古典的な話題ですが，コワレフスカヤが1900頃に剛体の運動の可積分なケースを発見してから，次に見つかった可積分な微分方程式が戸田格子であり，論文が出たのは1967年でした．可積分といっても解が書けること以外にもいくつかの良い性質を戸田格子は持っており，この研究以降さまざまな可積分系が発見されることとなりました．戸田格子の持ついい性質の一つとして，この記事ではLax形式で書けることを取り上げます．

Lax形式


戸田格子のハミルトン系を書き下すと以下のようになります．
\displaystyle\qquad \frac{d q_j}{d t} = p_j \\ \displaystyle \qquad \frac{d p_j}{d t} =\exp(q_{i+1} - q_i) - \exp ( q_i - q_{i+1})
ここで新たな変数 a_j, b_j を以下のように定義します．
\displaystyle \qquad a_j = \frac{1}{2} \exp \left( \frac{q_j - q_{j+1}}{2} \right) \displaystyle \qquad b_j = \frac{1}{2} p_j
この変数の方程式に書き換えると，微分方程式は
\displaystyle \qquad \frac{d a_j}{d t} = a_j ( b_j - b_{j+1} ) \\ \displaystyle \qquad \frac{d b_j}{d t} = 2 ( a_{j-1}^2 - a_j^2)
となります．綺麗にはなりましたが，この方程式のどこがいいのでしょうか？ここでさらに a_j, b_j で定まる行列 L, A を定義します．
\displaystyle \qquad L = \left( \begin{matrix} b_1 & a_1 & 0 & \dots & 0 & a_n \\ a_1 & b_2 & a_2 & \dots & 0 & 0 \\ 0 & a_2 & b_3 & \dots & 0 & 0 \\ & & & \ddots & & \\ 0 & 0 & 0 & \dots& b_{n-1} & a_{n-1} \\ a_n & 0 & 0 & \dots& a_{n-1} & b_n \end{matrix} \right) \\

\displaystyle \qquad A = \left( \begin{matrix} 0 & a_1 & 0 & \dots & 0 & -a_n \\ - a_1 & 0 & a_2 & \dots & 0 & 0 \\ 0 & - a_2 & 0 & \dots & 0 & 0 \\ & & & \ddots & & \\ 0 & 0 & 0 & \dots & 0 & a_{n-1} \\ a_n & 0 & 0 & \dots& -a_{n-1} & 0 \end{matrix} \right)
すると，微分方程式は
\displaystyle \qquad \frac{d L}{d t} = [ L, A]
と書くことができます．ここで [ L, A] = LA - AL です．この形の微分方程式をLax形式と呼びます．分かりづらいかもしれませんが， n が小さい時に具体的に書いてみると様子がわかります．例えば，3 自由度系，つまり， n = 3 のとき，
\displaystyle \qquad L = \left( \begin{matrix} b_1 & a_1 & a_n \\ a_1 & b_2 & a_2 \\ a_3 & a_2 & b_3 \end{matrix} \right), \qquad A = \left( \begin{matrix} 0 & a_1 & -a_3 \\ - a_1 & 0 & a_2 \\ a_3 & - a_2 & 0 \end{matrix} \right)
を使って計算してみてください．


Lax形式でかけた場合には，微分方程式の保存量をたくさん得ることができます．というのも任意の自然数 k に対して
\displaystyle \qquad \frac{d}{dt} \mathrm{Tr} L^k = 0
となるので \mathrm{Tr} L^k が保存量になります．ただし，保存量の全てが \mathrm{Tr} L^k と書けるわけではないですし， \mathrm{Tr} L^k が新しい保存量を次々と与えるとも限りません．しかし，戸田格子の場合にはこの手法で役に立つ保存量を得ることができます．これが戸田格子が可積分であることの根拠の一つを与えています．

一般化戸田方程式


この記事では，戸田格子の一般化の一つを考えていきます．戸田格子のハミルトニアンは
\displaystyle \qquad H = \frac{1}{2} \sum_{j=1}^n p_j^2 + \sum_{j=1}^{n-1} \exp (q_j - q_{j+1}) + \exp (q_n - q_1) \\
でした．ここで， n 個の n 次元ベクトル
\displaystyle \qquad \alpha_1 = (1, -1, 0 , \dots, 0)\\ \displaystyle \qquad \alpha_2 = (0, 1, -1, \dots, 0) \\ \qquad \qquad \vdots \\ \displaystyle \qquad \alpha_{n-1} = (0, \dots, 0, 1, -1) \\ \displaystyle \qquad \alpha_n = (-1, 0, \dots, 0, 1)
を用いれば，戸田格子のハミルトニアンは
\displaystyle \qquad H = \frac{1}{2} \sum_{j=1}^n p_j^2 + \sum_{k=1}^{n} \exp ( \alpha_k \cdot q ) \\
と書くことができます．ここで， \cdot は内積を表しています．このように，あるベクトルの集合 \{ \alpha_k \} を用いて
\displaystyle \qquad H = \frac{1}{2} \sum_{j=1}^n p_j^2 + \sum_{k=1}^{n} \exp ( \alpha_k \cdot q ) \\
書ける方程式を一般化戸田方程式と呼ぶことにします*1．つまり， \{ \alpha_k \} が質点の繋がり方を表しています．


一般化戸田方程式は戸田格子のようにいい性質を持っているとは限りません．そこで，二つの方向から一般化戸田方程式を研究することができます．

問題１ \{ \alpha_k \} に条件を課せば，（何らかの意味で）可積分になることを示せ．

問題２ （何らかの意味で）可積分であるときに， \{ \alpha_k \} が満たすべき条件を与えよ．

つまり，可積分であるための十分条件を与えるのが問題１で，可積分であるための必要条件を与えるのが問題２です．どちらの研究もあるのですが，今回は問題１に対応するBogoyavlensky(1976)の結果を紹介します．

（定理）
\{ \alpha_k \} が半単純リー代数の単純ルートであれば，一般化戸田方程式はラックス形式で書ける．

この記事の残りでは，この定理を説明していきます．まずはリー代数の知識を復習していきます．

リー代数

半単純リー代数


リー代数 \mathfrak{g} が半単純リー代数であるとは，単純リー代数の直和で書けることをいいます．単純リー代数とは自明でないイデアルを持たないリー代数のことでした．半単純リー代数の性質を使っていくだけなので，定義は気にしなくていいです．


リー代数 \mathfrak{g} の元 g \in \mathfrak{g} に対して，線形写像 \mathfrak{g} \to \mathfrak{g} が h \mapsto [g , h] が定まる．この写像を \mathrm{ad} (g) (h) := [g , h] と書き，随伴表現 と呼びます．つまり， \mathrm{ad} \colon \mathfrak{g} \to \mathrm{gl} (\mathfrak{g}) であり， \mathfrak{g} の基底を定めれば \mathrm{ad} (g) は行列で書くことができます．


この準備の下でカルタン部分代数を定義します．半単純リー代数 \mathfrak{g} の部分リー代数 \mathfrak{h} がカルタン部分代数であるとは以下の性質を満たすことをいう:

　(a.) 全ての元 h \in \mathfrak{h} に対して，随伴表現 \mathrm{ad} (h) は対角化可能である．

　(b.) \mathfrak{h} は(a.)を満たす部分リー代数の中で極大である．

性質(b.)から部分リー代数は極大ではあるものの最大とは限らないので複数存在するかもしれません．しかし，半単純リー代数の二つのカルタン部分代数 \mathfrak{h}_1, \mathfrak{h}_2 に対して，同型写像 \phi \colon \mathfrak{g} \to \mathfrak{g} で \phi(\mathfrak{h}_1) = \mathfrak{h}_2 となるものが存在するので，その意味で一意に定まると考えて良いです．（つまり，リー代数的に異なる意味を持つカルタン部分代数は存在しない．）さらにいい性質として，カルタン部分代数は可換になります．特に，(a.)の性質と組み合わせると， \mathrm{ad} (h) は同時対角化可能であることまでわかります．

ルート分解


以降， \mathfrak{g} のカルタン部分代数を \mathfrak{h} とします．ルート分解により簡単に表示することができます．ルートとはカルタン代数の元に対して随伴表現の同時固有値を与える \alpha \colon \mathfrak{h} \to \mathbb{C} です．厳密に言えば，ある x \in \mathfrak{g} が存在して，任意の h \in \mathfrak{h} に対して，
\displaystyle \qquad \mathrm{ad} (h) (x) = \alpha(h) x
が成り立つ \alpha がルートです．ルートは双対空間 \mathfrak{h}^* の元になっています．ルートの定義に現れる x は同時固有ベクトルを意味する重要なベクトルです．そこで，
\displaystyle \qquad \mathfrak{g}_\alpha = \{ x \in \mathfrak{g} \mid \mathrm{ad} (h) (x) = \alpha(h) x, \forall h \in \mathfrak{h} \}
とします． \mathfrak{h} は可換だったので， \mathfrak{h} \subset \mathfrak{g}_0 となります．さらに極大性から， \mathfrak{h} = \mathfrak{g}_0 も分かります． 0 でないルートの集まりをルート系といい \Delta と書くことにします．これを用いることで，リー代数は
\displaystyle \qquad \mathfrak{g} = \mathfrak{h} \oplus \sum_{\alpha \in \Delta} \mathfrak{g}_\alpha
と分解することができます．この分解をルート分解といいます．以降の考察で必要になる重要な性質を挙げておくと

\bullet 0 でないルートに対しては \mathfrak{g}_{\alpha} の次元は 1．
\bullet [ \mathfrak{g}_{\alpha}, \mathfrak{g}_{\beta} ] \subset g_{\alpha + \beta} ．特に， \alpha+\beta がルートでないならば， x \in \mathfrak{g}_\alpha, y \in \mathfrak{g}_{\beta} に対して [ x, y ] = 0．

コルート


ルートはカルタン部分代数の双対空間の元なので少し扱いづらいです．そこで内積を使って元の部分代数と同一視することを考えます．リー代数に対して， B(x, y) := \mathrm{Tr} ( \mathrm{ad} (x) \mathrm{ad} (y) ) で定まる双線型性形式 B \colon \mathfrak{g} \times \mathfrak{g} \to \mathbb{C} をカルタン・キリング形式といいます．これを部分代数に制限すると B \colon \mathfrak{h} \times \mathfrak{h} \to \mathbb{C} は \mathfrak{g} が半単純の時には非退化になることが知られています．これを用いれば， \mathfrak{h} と \mathfrak{h}^* を同一視することができます．つまり，ルートを \mathfrak{h} の元と考えることができます．厳密に言えば，全ての h \in \mathfrak{h} に対して
\displaystyle \qquad B( t(\alpha) , h ) = \alpha (h)
となる t(\alpha) が一意に決まるので，これをルート \alpha のコルートといいます*2 ．つまり，ルートをコルートだと思うことでカルタン部分代数 \mathfrak{h} に入っていると思うことができます．


これまではスカラーを複素数体 \mathbb{C} としましたが，実の空間で考えて良いことが知られています．特に， B は \mathfrak{h} の内積と考えることができるので，ルートはユークリッド空間に埋め込まれていると考えていいです． \mathfrak{h} の次元をリー代数のランクといいます．例として２次元のリー代数を考えている場合，ルートは 2 次元の空間で書くことができます．行列 \mathrm{sl}_{n+1} (\mathbb{C} ) = \{ A \in \mathrm{Mat}_n (\mathbb{C} ) \mid \mathrm{Tr} (A) = 0 \} はランク n のリー代数ですが， n = 2 の場合のルートは以下のように配置されます．

f:id:tetobourbaki:20190812171840j:plain
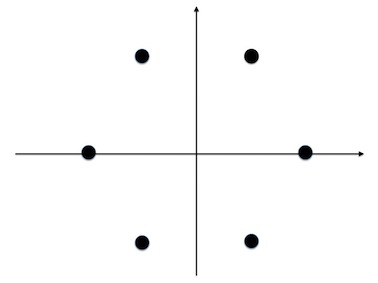
\mathrm{sl} (3) のルート
\mathfrak{h} が 2 次元で， 6 個のルートがあり，ルートそれぞれに 1 次元の空間 \mathfrak{g}_{\alpha} があるのでルート分解により \mathfrak{g} は 8 次元のベクトル空間です．私は， \mathfrak{h} 空間のルートそれぞれに 1 次元の空間が張り付いているものがリー代数 \mathfrak{g} であるとイメージしています．


また，シンプレクティック行列 \mathrm{sp}_n (\mathbb{C}) := \{ A \in \mathrm{Mat}_{2n} (\mathrm{C} ) \mid A^T J + JA = 0\}はランク n のリー代数で，n=2 の場合は以下のようになります．

f:id:tetobourbaki:20190812172026j:plain
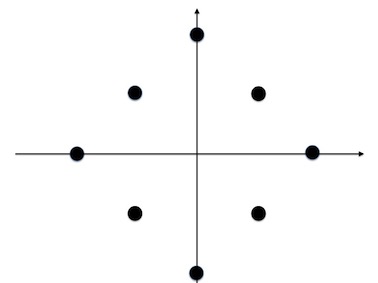
\mathrm{sp}(2) のルート

単純ルートと半単純リー代数の分類


カルタン部分代数の次元を m とします．このとき，ルート系 \Delta の部分集合 \{\alpha_k \}_{k=1}^m で以下の性質を満たすものが存在します:

（１） \{\alpha_k \}_{k=1}^m は \mathfrak{h}^* の基底である．
（２）任意のルートを \alpha = \sum_{k=1}^m c_k \alpha_k のように基底の線型結合で書いたとき，係数は全て整数 c_k \in \mathbb{Z} であり，
　全ての k で c_k \leq 0
または
　全ての k で c_k \geq 0
のどちらかが成り立つ．

この性質を持つ部分集合 \{\alpha_k \}_{k=1}^m を単純ルートと呼びます．仮定より，単純ルートの元 \alpha, \beta に対して \alpha - \beta は非ゼロルートにはなりません．あるルート \omega で \omega + \sum_{k=1}^n c_k \alpha_k, c_k \geq 0 がルートとなるのは全ての k で c_k = 0 の場合のみ，となる \omegaを極大ルートといいます．


半単純リー代数は単純ルートの幾何的な関係（原点からの長さと角度）で完全に決まることが知られています．行列の集まりで定義される４つのリー代数 \mathrm{sl}_{n+1} (\mathbb{C} )， \mathrm{o}_{2n + 1} (\mathbb{C} )， \mathrm{sp}_{n} (\mathbb{C} ), \mathrm{o}_{2n} (\mathbb{C} ) はそれぞれ A_n, B_n, C_n, D_n 型の単純ルートの配置から決定されます．また， E_6, E_7, E_8, F_4, G_2 型の単純ルートの配置も加えれば，半単純リー代数はこのいずれかのルートの配置に一致するということが知られています．あとでルートや単純ルートの配置を使うので，列挙しておきます． \mathbb{R}^n の標準基底を e_1, \dots, e_n と表すことにします．

（A_n 型）
\bullet \mathfrak{h}^* は \mathbb{R}^{n+1} の e_1 + e_2 + \dots + e_n に直行する平面
\bullet ルート系 \Delta = \{\pm ( e_i - e_j ), i < j \}
\bullet 単純ルート \{e_1 - e_2, e_2 - e_3, \dots, e_{n-1} - e_{n} \}．極大ルート e_1 - e_n．

（ B_n 型）
\bullet \mathfrak{h}^* = \mathbb{R}^{n}
\bullet ルート系 \Delta = \{\pm e_i, \pm ( e_i \pm e_j ), i < j \}
\bullet 単純ルート \{e_1 - e_2, e_2 - e_3, \dots, e_{n-1} - e_{n} , e_n \}．極大ルート e_1 + e_2．

（C_n 型）
\bullet \mathfrak{h}^* = \mathbb{R}^{n}
\bullet ルート系 \Delta = \{\pm 2e_i, \pm ( e_i \pm e_j ), i < j \}
\bullet 単純ルート \{e_1 - e_2, e_2 - e_3, \dots, e_{n-1} - e_{n} , 2e_n \}．極大ルート 2 e_1．

（ D_n 型）
\bullet \mathfrak{h}^* = \mathbb{R}^{n}
\bullet ルート系 \Delta = \{ \pm ( e_i \pm e_j ), i < j \}
\bullet 単純ルート \{e_1 - e_2, e_2 - e_3, \dots, e_{n-1} - e_{n} , e_{n-1} + e_n \}．極大ルート e_1 + e_2．

（ E_8 型）
\bullet \mathfrak{h}^* = \mathbb{R}^{8}
\bullet ルート系 \Delta = \{\pm ( e_i \pm e_j ), i < j, \frac{1}{2} \sum_{k=1}^8 (-1)^{m(i) } e_i , \sum_{k=1}^8 m(i) \text{は偶数} \}
\bullet 単純ルート \{\frac{1}{2}(e_1 + e_8 - \sum{k=1}^7 e_i, e_1 + e_2, e_2 - e_1, e_3- e_2, \dots, e_7 - e_6 \}．極大ルート e_7 + e_8．

（ E_7 型）
E_8 で e_7 + e_8 と直交するものをとったもの．ただし，極大ルートは e_8 - e_7

（ E_6 型）
E_8 で e_7 + e_8 と e_6 + e_8 に直交するものをとったもの．ただし，極大ルートは \frac{1}{2} (e_1 + e_2 + e_3 + e_4 + e_5 - e_6 - e_7 - e_8)

（ G_2 型）
\bullet \mathfrak{h}^* は \mathbb{R}^{3} の e_1 + e_2 +e_3 に直行する平面
\bullet ルート系 \Delta = \{ \pm ( e_i \pm e_j ), i < j, \pm (2 e_i - e_j - e_k), i \neq j \neq k \}
\bullet 単純ルート \{e_1 - e_2, - 2e_1 + e_2 + e_3\}．極大ルート 2e_3 - e_2 - e_1．

定理の意味と証明


Bogoyavlenskiの定理の意味を説明し，証明を与えましょう．

半単純リー代数 \mathfrak{g} とそのルート分解
\displaystyle \qquad \mathfrak{g} = \mathfrak{h} \oplus \sum_{\alpha \in \Delta} \mathfrak{g}_\alpha
を考えます．ランクを n とし， \mathfrak{h} の基底を h_1, \dots, h_n とします． \mathfrak{g}_\alpha は 1 次元なので，その基底を e_{\alpha} で表します．このとき， [ \mathfrak{g}_{\alpha}, \mathfrak{g}_{\beta} ] \subset g_{\alpha + \beta} やルートの定義などからリー括弧が以下のように計算できます．

\bullet \displaystyle [ e_{\alpha}, e_{\beta} ] = N_{\alpha, \beta} e_{\alpha, \beta} \\ \bullet \displaystyle [ e_{\alpha}, e_{-\alpha} ] = B(e_{\alpha}, e_{-\alpha}) t_{\alpha} \\ \bullet \displaystyle [ h_k, e_{\alpha} ] = \alpha (h_k) e_{\alpha} \\ \bullet \displaystyle [ h_j, h_k ] = 0
ここで， N_{\alpha, \beta} はある定数．ルート分解によりこの N_{\alpha, \beta} が定まれば， \mathfrak{g} のリー代数の構造が完全に決定できたことになります．


ここからが本題です．ルート系の部分集合 R := \{\alpha_1, \dots, \alpha_m \} を
　 i \neq j に対して， \alpha_i - \alpha_j が非ゼロルートにならない
となるようにとります．すると， N_{\alpha, \beta} = 0 となり， [ e_{\alpha}, e_{\beta} ] = 0 となります．単純ルートで R =\{\alpha_1, \dots, \alpha_n \} と定めれば， R はこの性質を満たします．さらに，この R に極大ルートのマイナスを追加した R =\{\alpha_1, \dots, \alpha_n, -\omega \} を考えてもこの性質を満たします．


Bogoyavlenskyの定理は正確には以下のような主張です．

（定理）
\mathfrak{g} をランク n の半単純リー代数とし，h_1, \dots, h_n をカルタン部分代数の基底とする．また，ルート系の部分集合 R := \{\alpha_1, \dots, \alpha_m \} が
　 i \neq j に対して， \alpha_i - \alpha_j が非ゼロルートにならない
を満たすとする．最後に B( e_{\alpha_i}, e_{-\alpha_i} ) = 1 となるように \mathfrak{g}_{\alpha_i} の基底 e_{\alpha_i} をとる．

このとき， t_{\alpha_i} = \sum_{j=1}^n d_{ij} h_j と書けたとすると，ハミルトニアン
\qquad \displaystyle H = \frac{1}{2} \sum_{k,l} B(h_k, h_l) p_k p_l + \sum_{k=1}^m \exp (2 \sum_{j = 1}^n d_{kj} q_j )
を持つハミルトン系はLax形式で書ける．特に， h_1, \dots, h_n をカルタン・キリング形式 B で定まる内積の正規直交基底にとると，Lax形式で書ける一般化戸田方程式が得られる．

ここで， t_{\alpha_i} = \sum_{j=1}^n d_{ij} h_j とは（コ）ルートを基底で表示しているということです．つまり，ルートの成分表示における成分 d_{ij} で，一般化戸田方程式の質点の繋がり方が決まります．

（証明）変数変換 x_k = \exp (\sum_{j = 1}^n d_{kj} q_j ) を考えると，ハミルトン系は
\displaystyle \qquad \frac{d x_k}{dt} = x_k \sum_{ i , j } d_{kj} p_i B(h_i, h_j ) \\ \displaystyle \qquad \frac{d p_k}{dt} = -2 \sum_{j=1}^m x_j^2 d_{jk}
と書けることがわかる．ここで， \mathfrak{g}の元を
\displaystyle \qquad L := \sum_{k=1}^m x_k (e_{\alpha_k} + e_{-\alpha_k} ) + \sum_{j=1}^n p_j h_j \\ \displaystyle \qquad A := \sum_{k=1}^m x_k (e_{\alpha_k} - e_{-\alpha_k} )
と定めれば，微分方程式は
\displaystyle \qquad \dot{L} = [L, A ]
と書けることがわかる．このリー括弧の計算では
\bullet \displaystyle [ e_{\alpha_i}, e_{\alpha_j} ] = 0\\ \bullet \displaystyle [ e_{\alpha_i}, e_{-\alpha_i} ] = t_{\alpha_i} \\ \bullet \displaystyle [ h_k, e_{\alpha_i} ] = \alpha_i (h_k) e_{\alpha_i} \\ \bullet \displaystyle [ h_j, h_k ] = 0
用いるだけで証明ができる．最後に，半単純リー代数は同じ型を持つ行列の集合で定義されたリー代数と同型なので，
\displaystyle \qquad \dot{L} = [L, A]
のリー括弧が行列のリー括弧で書ける． \square


前節の最後に単純ルートや極大ルートがどのように書けるかを書きましたが，それを用いれば以下のような一般化戸田方程式を得ることができます．記述を簡単にするために
\displaystyle \qquad V_n = \sum_{i=1}^n \exp (q_i - q_{i+1})
とおくと，
\displaystyle \qquad H_{A_n} = \frac{1}{2} |p|^2 + V_n + \exp(q_{n+1} - q_1) \\ \displaystyle \qquad H_{B_n} = \frac{1}{2} |p|^2 + V_{n-1} + \exp(q_{n} ) \exp(- q_1 - q_2) \\ \displaystyle \qquad H_{C_n} = \frac{1}{2} |p|^2 + V_{n-1} + \exp(2 q_n) + \exp(-2 q_n) \\ \displaystyle \qquad H_{D_n} = \frac{1}{2} |p|^2 + V_{n-1} + \exp(q_{n-1} + q_n) + \exp(-q_1 - q_2) \\ \displaystyle \qquad H_{A_n} = \frac{1}{2} |p|^2 + \exp (q_1 - q_2) + \exp(-2 q_1 + q_2 + q_3) + \exp(q_1 + q_2 - 2 q_3)
ここで，R として単純ルートに極大ルートを加えたもので考えていますが，ポテンシャルの最後の項を除いたものは R として単純ルートをとった場合に対応します．


細かいことを言えば，定理を使うだけでは説明できない部分もいくつかあるのですが（例えば，A_n や G_2 は q と p の個数が違う），細かい注意はラックス形式を具体的に計算しながら見ていきます．

具体例での計算

暇があるときに書きます．

最後に

今回は，可積分であるための十分条件から一般化戸田方程式を説明しましたが，可積分であるための \{\alpha_k \} の必要条件を与える研究にも面白いものがあります．特に以下の論文が基本的です．
　Kozlov, Treshchev, Polynomial integrals of Hamiltonian systems with exponential interaction, 1990.
関連する話題には自分の専門に関係した話もあるので，機会があれば一般の人も参加できるような勉強会・研究集会で一度話したいと思っています．そのような場で発表できる機会があればご連絡いただけると嬉しいです．

参考文献

　Bogoyavlensky, On perturbation of the periodic Toda lattice, 1976.
　大貫，吉田，岩波講座　現代の物理学１　力学．
　佐藤，リー代数入門．

*1:一般化戸田方程式の定義はまちまち．特に可積分なものをそう呼ぶかもしれない

*2:異なる意味でコルートという用語を使うことも多いので注意．