記号の世界ゟ

このブログでは, 数学書などの書評を書きます。また、受験などの勉強法をまとめます。

整数の分割とヤング図形（可積分系入門）

可積分

この記事の続きですが，本記事だけで楽しめます．
tetobourbaki.hatenablog.com
当分は可積分理論に現れる基本的な手法を見ていきます．

組み合わせ問題

組み合わせ問題は一般に解くことが難しいです．組み合わせ問題の面白さというのは、全ての組み合わせを数えれば原理的には答えを求めることができるものの，それは計算機を使ってすら難しいところでしょう．

以下の動画を見れば，簡単そうな問題でも数え上げると大変なことになることが分かります．

次の動画では，簡単に計算するソフトを紹介しています．数学の力を使えばこんなことが可能になるのですね．

今回はこの問題ではなく、整数の分割を取り上げます。

整数の分割

整数の分割とは，与えられた自然数を自然数の和で書くことです．
例えば，3は
\displaystyle 3 = 1+1+1\\ 3 = 2+1\\ 3 = 3
の 3通りの分割法があります．

もう少し正確に定義しましょう．和の順番を変えても同じ分割だと考えることにするので，和を書くときは大きい数字の順に並べることにしましょう．すると以下のように定義ができます．

定義
自然数 Nの分割とは自然数の列 a_1 \geq a_2 \geq \dots \geq a_nを用いて書ける
\displaystyle N = a_1 + a_2 + \dots + a_n
のことを言う．このときの a_iを和因子という．

4 の分割を並べてみると，
4 = 1 + 1 + 1 + 1\\ 4 = 2 + 1 + 1 \\ 4 = 2 + 2 \\ 4 = 3 + 1\\ 4 = 4
の 5通りがある．
5の分割を並べてみると，
5 = 1 + 1 + 1 + 1 + 1\\ 5 = 2 + 1 + 1 + 1\\ 5 = 2 + 2 + 1 \\ 5 = 3 + 1 + 1\\ 5 = 3 + 2\\ 5 = 4 + 1\\ 5 = 5
の 7通りがある．
分割の数を分割数という． Nの分割数を p(N)と書く．
ここまでの例では分割数はそれほど大きくならないようにも見える．しかし，分割数は爆発的に大きくなる．
p(6) = 11であるが，分割数が 100を越えるのは N = 13の時で p(13) = 101である． 100の分割数は p(100) = 190,569,292でありずいぶん大きい． 1000の分割数になるととてつもなく大きくて， 31桁の自然数となる．

分割数が面白くなるのは、単に全ての分割を考えるのではなく、分割に条件をつけた場合の分割数である．（ラマヌジャンはこの分野でたくさん業績があるらしい．）例えば，全ての和因子が 2以上という条件をつけると，上に列挙したものをみれば， 5の分割数は 2となり非常に小さくなることが分かる．この方向で面白く深い問題を考えるのは次回以降の記事に回すことにして，次にヤング図形という便利な道具を導入しよう．

ヤング図形

ヤング図形とは以下のような箱の集まりでできる図形のことである．２つ例を挙げる．
\qquad f:id:tetobourbaki:20180220223648p:plain

\qquad f:id:tetobourbaki:20180220223651p:plain
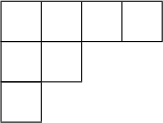
適当に箱を並べたのではなくルールがある． i行目に並べた箱の個数を b_iと表すことにすると， b_1 \geq b_2 \geq \dots b_nが成り立つ必要がある．つまり下の行は上の行より多くの箱を並べてはダメだということである．最初の例では，
b_1 = 3, \quad b_2 = 1, \quad b_3 = 1, \quad b_4 = 1
であり， 2番目の例では
b_1 = 4, \quad b_2 = 2, \quad b_3 = 1
となっている．ヤング図形のルールを見れば分かるように，ヤング図形は整数の分割を表している．最初の例は 6の分割 3 + 1 + 1 + 1を表しており， 2番目の例は 7の分割 4 + 3 + 1を表している．数の分割とヤング図形は一対一に対応していることが分かる．

ヤング図形を線対称にひっくり返したものを共役という．（線は左上から右下への斜めの線にとる．）
言葉では分かりにくいので，例で説明する．上で挙げた最初の例とその共役を並べると
\qquad f:id:tetobourbaki:20180220223648p:plain \qquad f:id:tetobourbaki:20180220225159p:plain \qquad f:id:tetobourbaki:20180220225008p:plain
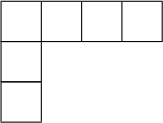
である． 2番目の例とその共役を並べると，
\qquad f:id:tetobourbaki:20180220223651p:plain \qquad f:id:tetobourbaki:20180220225159p:plain \qquad f:id:tetobourbaki:20180220225515p:plain
である．ヤング図形の共役はやはりヤング図形になっていることが分かる．つまり，分割をヤング図形と考えて，その共役を取ることで新しい共役を得ることができる．この操作はヤング図形を使わなくても定義できるものの，ヤング図形を使うとイメージが湧く．

応用

行の個数が m個以下のヤング図形を考えよう．これは和因子の個数が m個以下になる分割を考えていることになる．一方，その共役をとると，「行の個数が m個以下」のヤング図形の共役は「それぞれの行の箱の数が m個以下」のヤング図形になる．これは全ての和因子が m以下の分割に対応する．このことを踏まえると以下の定理が成り立つ．

定理
自然数 Nに対して，和因子の個数が m個以下になる Nの分割数と，全ての和因子が m以下の Nの分割数は等しい．
このことを N = 5, m = 3で確認しよう．
和因子の個数が 3個以下になる 5の分割は
5 = 2 + 2 + 1 \\ 5 = 3 + 1 + 1\\ 5 = 3 + 2\\ 5 = 4 + 1\\ 5 = 5
の 5個である．一方，全ての和因子が 3以下の Nの分割
5 = 1 + 1 + 1 + 1 + 1\\ 5 = 2 + 1 + 1 + 1\\ 5 = 2 + 2 + 1 \\ 5 = 3 + 1 + 1\\ 5 = 3 + 2\\
の 5個であり，確かに定理が成り立つ．

共役を使えば色々定理が作れそうである．

まとめ

今回は整数の分割を通して，ヤング図形を導入しました．ヤング図形は可積分理論の様々な場面で現れますが，それは整数の分割を表すと覚えておくと，損はないでしょう．

次回はq類似とかqアナローグとか呼ばれるものを導入します．これも可積分理論でよく使われるものですが，整数の分割とも関係の深い分野です．

続き
tetobourbaki.hatenablog.com